Non-determinism

Posing delayed, but for a few days now I have had support for further non-determinism.  To exemplify I have modeled a few new windows and added the corresponding mappings.  In the grammar:

grammar:

    s gv

    s gh

    g df

    f bf

    v bwq

    q bwq

    q wzq

    q wxq

    q cwq

    h bwwe

    e bwwe

    e bwbe

    e bxbe

    e bcwe

    e bzxe

    e cbwe

end

mapping:

    d TestArchDoor

    b TestWall

    w TestWindow

    z TestQuadWindow

    x TestBevelWindow

    c TestRoundWindow

end

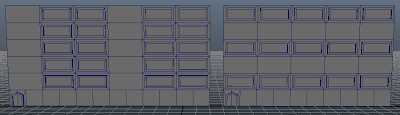
Running that grammar produces this building:

Up next is the simulated annealing.  For a simple test I'll compare each element to its neighbors and let it probably become the same as the most frequent neighbor.  There will be a decreasing probability of each of the subsequently less frequent neighbors that will also fall off as the temperature decreases.  To make sense of that lets cover simulated annealing briefly.  The basic idea stems for annealing in metallurgy where a metal is cooled slowly to create big crystals with fewer defects.  In each iteration of the annealing loop elements are allowed change based on some set of contextual rules and the current temperature.  The higher the temperature the more drastic the changes can be.  In the further spirit of non-determinism these changes also have a random component but will err towards stability as the temperature decreases.  To make sure the changes are useful a cost function is also introduced to evaluate each state. That can ensure that new states are "better" than the old ones.  The process ends when the temperature gets too low for meaningful changes to take place or some cost threshold is crossed.  To test it out I'll be making elements turn into their most frequent neighbors which should result in a completely uniform building.

Lets see how that goes!

More Thoughts About Grammars and Buildings

Grammatical constructions complete!  Using the idea of a formal grammar evolving a string of symbols (letters) into a new string of symbols we can make use of two categories: terminal and non-terminal symbols.  Terminals have associated geometry specified in the mapping section and non-terminals evolve into a new string of symbols.  For clarity I have reserved a few symbols: 's' is the start symbol, 'g' is the ground floor, 'v' creates a column based layout, 'h' creates a row based layout.  The evolutions or children of these symbols still need to be defined in the rules of the grammar, but these will have special behavior without extra rules.  Rules take the form: "symbol child_string" where multiple instances of the same symbol create multiple children.  The mapping section defines its symbols as terminals and gives the name of the element from the library that they map to.  Terminals can only have one mapping, randomality should be introduced with a non-terminal that have multiple non-terminals as children.  These building show row and column based layouts built from the following grammar.

From the input file:

grammar:
    s gv //start rules
    s gh
    g df //ground floor rules
    f bf
    v bwq //vertical rules
    q bwq
    h bwwe //horizontal rules
    e bwwe
end

mapping:
    d TestArchDoor
    b TestWall
    w TestWindow
end

Here 'f'', 'q', and 'e' are non-terminals that serve only to repeat their patterns.  The building on the left is from the horizontal rule 'e' with a wall and two windows repeating in each row.  On the right 'q' alternates walls and windows in each column.  From here the next step is to test increased randomality by adding more symbols and terminal geometry.