Non-determinism

Posing delayed, but for a few days now I have had support for further non-determinism.  To exemplify I have modeled a few new windows and added the corresponding mappings.  In the grammar:

grammar:

    s gv

    s gh

    g df

    f bf

    v bwq

    q bwq

    q wzq

    q wxq

    q cwq

    h bwwe

    e bwwe

    e bwbe

    e bxbe

    e bcwe

    e bzxe

    e cbwe

end

mapping:

    d TestArchDoor

    b TestWall

    w TestWindow

    z TestQuadWindow

    x TestBevelWindow

    c TestRoundWindow

end

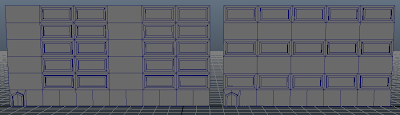
Running that grammar produces this building:

Up next is the simulated annealing.  For a simple test I'll compare each element to its neighbors and let it probably become the same as the most frequent neighbor.  There will be a decreasing probability of each of the subsequently less frequent neighbors that will also fall off as the temperature decreases.  To make sense of that lets cover simulated annealing briefly.  The basic idea stems for annealing in metallurgy where a metal is cooled slowly to create big crystals with fewer defects.  In each iteration of the annealing loop elements are allowed change based on some set of contextual rules and the current temperature.  The higher the temperature the more drastic the changes can be.  In the further spirit of non-determinism these changes also have a random component but will err towards stability as the temperature decreases.  To make sure the changes are useful a cost function is also introduced to evaluate each state. That can ensure that new states are "better" than the old ones.  The process ends when the temperature gets too low for meaningful changes to take place or some cost threshold is crossed.  To test it out I'll be making elements turn into their most frequent neighbors which should result in a completely uniform building.

Lets see how that goes!

More Thoughts About Grammars and Buildings

Grammatical constructions complete!  Using the idea of a formal grammar evolving a string of symbols (letters) into a new string of symbols we can make use of two categories: terminal and non-terminal symbols.  Terminals have associated geometry specified in the mapping section and non-terminals evolve into a new string of symbols.  For clarity I have reserved a few symbols: 's' is the start symbol, 'g' is the ground floor, 'v' creates a column based layout, 'h' creates a row based layout.  The evolutions or children of these symbols still need to be defined in the rules of the grammar, but these will have special behavior without extra rules.  Rules take the form: "symbol child_string" where multiple instances of the same symbol create multiple children.  The mapping section defines its symbols as terminals and gives the name of the element from the library that they map to.  Terminals can only have one mapping, randomality should be introduced with a non-terminal that have multiple non-terminals as children.  These building show row and column based layouts built from the following grammar.

From the input file:

grammar:
    s gv //start rules
    s gh
    g df //ground floor rules
    f bf
    v bwq //vertical rules
    q bwq
    h bwwe //horizontal rules
    e bwwe
end

mapping:
    d TestArchDoor
    b TestWall
    w TestWindow
end

Here 'f'', 'q', and 'e' are non-terminals that serve only to repeat their patterns.  The building on the left is from the horizontal rule 'e' with a wall and two windows repeating in each row.  On the right 'q' alternates walls and windows in each column.  From here the next step is to test increased randomality by adding more symbols and terminal geometry.

Grammars

Before moving into grammatical generation of elements, there are important questions to answer   Should the grammar generate floors or columns?  Should it be context sensitive?  SHould pattern conflicts between adjacent floor or columns be resolved in the simulated annealing step (by the way, I'll be using simulated annealing)?
For now the start symbol with generate a ground floor and either a set of rows or columns.  By supporting both randomly there should be different emergent patterns to widen the variety of buildings generated.  The basics of the grammatical approach should not be too complicated.  Each symbol with evolve randomly into one of its descendants and then branching string will be terminated then the row or column has run out of the respective dimension on the building.  Here setting width and height as floats rather than a fixed number of floors will work better.

As part of the simulated annealing step I am considering a unordered "element soup" approach incase the user specifies elements that span multiple floors wants an element of out of normal alignment.  Pending better understanding of how the annealing step works this idea will be reviewed.

Non Uniform Scale

When I say non uniform scale I am not referring to the different axes having different scale factors, I mean scaling along a single axis non uniformly.  Towards that end I have added to my definition of an element (door, window, etc.) optional anchor points.  Given a target value, anything before the lower anchor point on a given axis is left in place, anything after is translated so that the furthest point (bounding box maximum) reaches the target, and anything in the middle gets LERPed along.

These elements have kept their original thin frames but have still grown to fill the target spaces defined by floor height and given (or default) widths.  However, not all of these are supposed to be of the full floor height according to the configuration file (unchanged since last post).  The next step is to let them rest at the base of the floor and move only the points within epsilon error of the top bounding box up to fill the remaining height.

Here windows with locked aspect ratios remain square as modeled and their top points fill in vertically.  The next mini-feature will be justification.  I want to be able to lift elements off of the floor baseline and then fill downwards as needed.

Now with content!

It turns out AMPL is definitely overkill for the majority of this project.  It may still be useful in the future to resolving conflicting elements when multiple content generation methods are working at once, but for now direct code will work better.  Having moved into C++ is was relatively simple to get test geometry distributing according to a user supplied configuration file.  Currently the program reads in a configuration file and library of elements and the produces a single composite OBJ file from instances of the elements following the rules in the configuration file.  My current visualization strategy is to drop it into Maya.  Example time!

These two facades were produced by altering the proportions of the bottom right door.  On the left the width is unconstrained, so it stays narrow and a second door fits.  On the right the door is locked to a 2:3 ration and the second door no longer fits.  Lets look at the file with the change in indicated:

GLobals:
    output test.obj
    width 10
    depth 3
    type facade
    floors 2 height 3
    style test
end
Floor 0:
    element door lockAspect
    element wall width .5
    element window width 2
    element wall
    element door lockAspect aspect .6666
    element wall
    element door
end
Floor 1:
    height 2
    element wall
    element window width
    element wall width 5
    element window width 
end
floor 2:
    element wall width 3
    element window
    element wall
    element window width 5
end

There are a few stability things going on here.  The global number of floors is overridden by the definition of another floor, later there should be tools for selecting which floors to use or repeat.  Floor 1 is overriding the global floor height just to prove that it works.  Additionally, each element can optionally set fixed width, height, aspect ratio  locked default aspect, etc.  All of those values have defaults and if left unset have logic to  adjust them to the building's needs.  Any elements that does not fit in the building width gets ignored and any leftover space gets filled with blank wall.

It is a personal goal to make as many arguments and constraints optional as possible to leave this system as flexible as possible.  Next up, filling in those awkward gaps around short elements and getting nonuniform scaling to that bigger elements don't have thicker frames (also maybe vertical alignment options).

Mini update: Doric Column

Given the footprint dimensions (X,Y) I can now compute the height (Z), base diameter (baseD), and top diameter (top) of a Doric Column.  Using the same relations it is equally easy to compute the area and diameters from the desired height.

Sample output:

21 iterations, objective 96000
Nonlin evals: obj = 25, grad = 24, constrs = 25, Jac = 24.
X = 20
Y = 30
Z = 160

baseD = 20
topD = 16

To kick things off I'll be experimenting with AMPL (A Modeling Language for Mathematical Programming). So far I have discovered that the solver I am using have some oddities when I allow variables to be too small (less than .01) but if I pick the right totally arbitrary modeling units I should be fine.  Heres the fun part: what to look for next.  The first test will be to solve the proportions of a doric column from its radius.  The next test is to compute the various sizes of the largest Parthenon that will fit on a given footprint.